Глава 5
Что еще такое хаос?
Нелинейность
Ко времени, когда исследования хаоса приобрели статус повсеместности, уважаемый журнал «Физика», уже освещавший некоторый аспекты из трех других журналов, представил четвертую серию, «Физика D», посвященную нелинейным феноменам. Этот шаг был сделан спустя несколько лет после основания еще одного журнала «Нелинейный анализ: Теория, Методы и Применения». Несколько лет спустя первый том в серии «Нелинейности» появился. Люди, вложившие силы в него, представили множество дисциплин, и пришли из многих институтов, включая Центр Изучения Нелинейности в национальной лаборатории Лос Аламоса, центр нелинейной динамики из университета Техаса, и институт нелинейной науки из университеты Калифорнии. Так что же такое они вложили? По большей части это был хаос.
Разве «нелинейность» и «хаос» - синонимы? Не совсем. Прежде всего, различаются слова по своему значению. Линейный процесс – это такой процесс, при которой любое изменение переменной в начале действия создает изменения в том же диапазоне или приблизительно таком же в последующее время. То есть, если нечто сначала изменилось вдвое, то и последующие изменения будут вдвое. Вы можете подставить «половину» или «в пять раз» или «сотни раз», всегда описание будет правильным. Из этого следует, что если поздние значение любой переменной построены относительно начальных значений любой переменной на графике, точки будут лежать строго на прямой линии – отсюда и название. Нелинейный процесс – это просто такой процесс, который не совсем линеен.
Возможно самым лучшим примерном настоящего линейного процесса послужит то, что мы сами можем создать. Простой пример, стоимость еды или любой другой вещи, предполагается, что на них нет скидки и нужно купить их по высокой цене. Если мы купим дюжину яиц и покинем магазин на доллар меньше, чем если бы мы не совершали покупки, кто-то еще может купить две дюжины яиц того же размера и качества, выйдя из магазина с минус двумя долларами.
Поскольку их поведением управляют некоторые конкретные физические систему, то получается, что оно строго линейно. Огромная важность значения линейности лежит в области сочетания двух обстоятельств. Первое, множество материальных феноменов ведут себя приблизительно линейно, так что полезные линейные математические модели могут симулировать их поведение. Маятник качается с небольшим углом и представляет собой почти линейную систему. Второе, линейные уравнения могут быть выведены множеством способов, которые не работают в нелинейных уравнениях.
Довольно легко увидеть, даже без проведения долгого математического анализа, что модель снежного склона нелинейна. Рассматривая доску, которая начинает движение из состояния покоя в точке 1 метр восточнее возвышения, мы начнем скользить в направлении более крутого спуска. И таким образом мы все дальше и дальше будет отклоняться от юго-восточного направления. Рассмотрим вторую доску на 5 метров восточнее от того же холма. Она будет вести себя точно так же как и первая, поскольку она на 1 метр от следующего холма.
Если бы система была линейной, третья доска, стартовав между первыми двумя должна бы проходить посередине и также двигаться на юго-восток. Однако, поскольку она стартует в метре от второго холма, то вероятнее будет двигаться более или менее на юго-запад.
Те же причины показывают, что любая хаотичная система должна быть нелинейной, обеспечивая каждой переменной системы свои ограничения. Такой переменной может стать температура в Фениксе, которая независимо от того, что чувствуют люди, не может достичь точки кипения или выпасть в океан, рядом с центральной Аляской. Если глобальный погодный шаблон действительно чувствителен к взмахам крыльев бабочки, тогда рано или поздно наступит момент, когда температура в Фениксе будет на 10 градусов выше, чем должна быть без помощи этого насекомого, а по системе линейности, взмахи чаек (в 1000 раз сильнее бабочек), должны тогда создать температур на 1000 градусов выше – что явно невозможно.
Даже если погода не зависит от крыльев бабочки, аргумент все еще имеет право на жизнь. Хаотичная система такова, что в ней даже самое мельчайшее изменение в настоящем, может привести к огромным изменениям в будущем. Если бы такая система была нелинейной, то умеренные отличия от приемлемой формы, должны были бы произвести такие огромные эффекты, какие вряд ли вообще возможны.
И даже несмотря на то, что хаос тяготеет к нелинейности, нелинейность еще не означает хаос. Простой пример представляет вам эту очевидную разницу, это известный нам снежный склон, с высотой холмов такой, что они возвышаются над ямами на 50 см. В этом случае мы видим, что доска, возможно псле некоторых колебаний вперед и назад, продолжит движение на юго-восток, или на юго-запад в особой иррегулярной манере. Легкое вмешательство в это состояние создаст новую траекторию движения, что однако вскоре вернется к прежнему курсу.
Особенно удивительным может показаться, что последовательное поведение системы может измениться, когда интенсивность какого-то влияния проходит критический уровень. При более детальном рассмотрении бифуркаций можно увидеть, что хаос на снежном склоне может вновь возникнуть, если холмы будут 43 см высотой, и исчезнет, как только холмы станут 40 см. Этот пример не так удивителен, чем тот, что может ожить нас, когда мы войдем во владения нелинейности.
Комплексность
На следующих страницах мы увидим три рисунка, два созданы компьютером и одна фотография. Какое из этих изображений более комплесное?
Если вы вместе с другом сравните свои ответы и не найдете понимания, но не стоит беспокоиться. Термин «комплексность» имеет почти столько же определений, сколько «хаос».
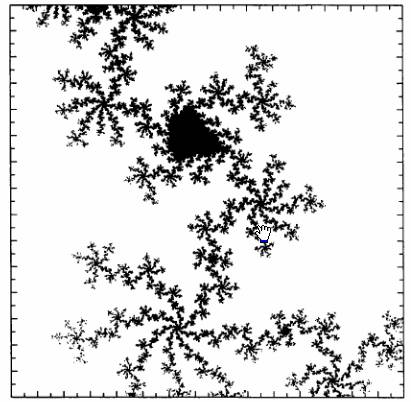
Трудно себе представить боле комплексную систему, в нетехническом смысле слова, чем система на Рисунке 54, где показаны мельчайшие частицы. Эта удивительная система – множество Мандельброта. На рисунке она сопровождается достаточным количеством точек, чтобы стать видимой. При большем увеличении окружающих точек, могут возникнуть какие-то вполне знакомые формы, где некоторый женщины могут рассмотреть звездочки, бриллианты и морских коньков.

Рисунок 54. Малая часть множества Мандельброта, с достаточно большим числом окружающих точек, чтобы сделать его видимым. Область вытянута по горизонтали от -0.664 до -0.634 и по вертикали от -0.498 до 0.468
Множество Мандельброта это достаточно простая математическая концепция. Чтобы нарисовать такую картинку, мы сделали одно место на плоскости «источником», и выбрали другое место в качестве «ключевой точки». Когда затем мы позволили точке из источника «прыгнуть» на плоскости, то в соответствии со специальным правилом, определяющим, что место из которого точка прыгнула, определяется в терминах ключевой точки и точки из которой она прыгнул. Данное правило появляется в обсуждении логического уравнения в Приложении 2. Первый прыжок, случайно заканчивается в ключевой точке. Если точка остается в рамках заданной области, окружающей источник, ключевая точка лежит во множестве Мандельброта, и мы можем ее построить. Затем мы повторяем процедуру для каждого из больших скоплений ключевых точек, без изменения исходной точки или правило ею управляющего.
Кто-то может вообразить, что точка, чья ключевая точка за пределами множества прыгнула бы, как одна из тех, у которых ключевая точка поблизости, просто внутрь, по меньшей мере. Так действительно может быть; точки, чьи ключевые точки недалеко за пределами могут совершить множество прыжков, выйдя за пределы обозначенных областей. Чтобы создать фигуру, я взял два миллиона ключевых точек, случайно выбранных из области, покрытой фигурой, я построил эти ключевые точки, 83 423 всего и ассоциировал их с точками прыжков, с запасом прыжков в 68 штук.
Что может быть более комплексно, чем множество Мандельброта? Возможно весь глобальный погодный шаблон – возможно анатомия отдельного человека.

Рисунок 55. Вариант японского аттрактора.

Рисунок 56. Полосы и шгтрихи на поле слежавшегося снега.
Как только началось изучение нелинейности, появились такие центры комплексных системных анализов в университете Иллинойса, и комплексная системная теория ветвей исследовательской лаборатории в Вашингтоне. Как только журналы заинтересовались нелинейностью, сразу появились такие журналы, как «Комплексные системы» в 1978 году. Изучение нелинейности во многом – это изучение хаоса. Действительно, комплексность иногда используется для указания ощутимой зависимости и всего того, что с ней происходит.
Согласно этому определения Рисунок 55 более комплексный. Это один представитель большого семейства странных аттракторов, открытых Йошисуке Уеда из университета Киото. Подобно Кэтрайт-Литлвудскому аттрактору на Рисунке 32, этот участок Пуанкаре аттрактора периодически создает диссипативную систему – в данном случае, так называемый осциллятор Дуффинга – но здесь видимое сходство заканчивается. Уеда обнаружил свидетельство странного поведения в начале 1961 году, но картинку с высокой степенью разрешения удалось получить только спустя время, как появились мощные компьютеры. Недавно он представил живое описание сложностей, с который он столкнулся, пока его идея была принята. В итоговой статье, Дэвид Рул описал оригинальный аттрактор Уеды как самый эстетически приятный из странных аттракторов, когда либо созданных – Рисунок 55 представляет собой несколько гротескное изображение – и он называл это не иначе, как японский аттрактор, но недавний визит в лабораторию Уеды в Киото, дало мне понят, что это было не совсем точное название – это более чем Японский аттрактор.
В сравнении с множеством Мандельброта, последнее не является последовательным множеством с точки зрения хаотичного поведения. Большинство прыгающих точек, чьи ключевые точки находятся во множестве не имеют ощутимых зависимостей в своих прыжках, и они скорее прыгаю приблизительно в периодической последовательности. Единственное исключение составляют точки, чьи ключевые точки находятся на границе множества.
Иногда между «хаосом» и «комплексностью» ставят такое различие, как нерегулярность во времени и пространстве. Два типа нерегулярности часто сопровождают друг друга, как например, турбулентные потоки.
Комплексность часто используется в несколько ином значении, когда указывается на длительность множества инструкций, которые должны бы обрисовать или сконструировать систему. С этой точки зрения Рисунок 56 более комплексный. Он выглядит больше как часть странного аттрактора – темные синусовидные кривые, отделённые широкими светлыми пространствами, а некоторые очевидные кривые можно увидеть ближе как пары кривых. Однако мы действительно смотрим на штрихи ветра на плотном снегу, покрывшего реку Сэдбери на востоке Массачусетса одним утром 1977 года.
На Рисунках 54 и 55 можно легко воспроизвести последующие краткие множества инструкций или создать короткие компьютерные программы, но штрихи не подчиняются ни одной простой известной математической формуле. Чтобы создать их числовым методом, мы должны будем определить местоположения такого множества точек на каждом штрихе, что все вокруг будет заполнено интерполяцией. Если бы мы могли взглянуть на выступы краев, то можно было бы подумать о том, что есть некие правила, по которым штрихи должны появиться в определенном месте, чтобы их сфотографировать. Однако эти штрихи вскоре исчезли и когда мы с женой гуляли здесь через несколько дней, их просто не было.
Фрактальность
Существуют уравнения, которые могут быть измерены только целыми числами – количество детей в семье, хотя мама на сносях может сказать, что теперь их два с половиной, число пробежек в бейсбольном матче, число букв в слове. Большинство людей включает сюда также количество измерений объекта или фигуры; трехмерный мяч может иметь двухмерную тень с одномерным контуром. Ближе к концу девятнадцатого века, однако, математики открыли, что некоторые множества точек имеют дробную мерность. В действительности случилось то, что некоторые ученые исследовали структуры, которые были несколько странными, и в результате обнаружилось, что эти объекты довольно трудно описать в виде простейших геометрических фигур в двух или большем количестве измерений. Тогда они перераспределили мерность так, что кривые, плоскости и твердые тела остались в одно-, двух- и трехмерном пространстве, тогда как точные значений переменных мерностей стали относится к менее известным структурам. Во многих случаях эти значения были дробными. Были представлены последовательности сходных логических определений; другие определения с этим не всегда согласовывались.
Одной из наиболее часто повторяемых проявлений этого рода было явление, представленное в 1919 году немецким математиком Феликсом Хаусдорфом. Модифицированное определение, которое я нашел как самое простое для понимания и которое равно Хаусдорфскому определению для множества точек, но больше других, это способность, представленная русским математиком Андреем Колмогоровым. Я буду ссылаться к нему, как к пространству. Его очень легко проиллюстрировать, когда точки множества лежат на плоскости, и окружены квадратом, скажем со стороной в один метр.
Мы разделим квадрат на четыре малых квадрата, каждый будет иметь сторону в полметра. Затем разделим каждый из новых квадратов еще на четыре квадрата, с одной четвертью метра на сторону и так далее. При каждом таком делении количество мы заметим, как возрастает количество всех точек множества. Нам интересно здесь то, насколько сильно вырастет это число после множества этапов.
Если множество точек, чье измерение равно целому внутреннему квадрату, или одной или более заполненной области, число квадратом незамедлительно или равномерно учетверяется при каждом шаге. Происходит увеличение при 2 в степени 2. Если это кривая или бесконечное число кривых конечной длины, количество просто постоянно удваивается, поскольку большинство новых малых квадратов будет лежать между кривыми. Происходит увеличение на 2 в первой степени. В итоге, если это одиночная точка или конечное множество точек, количество перестанет расти. Произойдет увеличение в 2 раза в степени 0. В каждом случае, по фактору экспоненты, 2, в которому диаметр квадрата уменьшается при каждом шаге, все это представляет пространственное множество.
А теперь спросим себя, существуют ли множества, в которых количество квадратов может бесконечно расти в 2 раза в степени d, где d не целое число. Если это возможно, то множество измерений, в данном случае d, это фракталы.
Такие множества совсем не сложно создать. Рассмотрим, например, то что получилось, если начать с простого квадрата, а затем произведя деление каждого квадрата на четыре маленьких квадратики и создавая при этом множество других квадратов. Первый шаг создаст большую букву L, второй сделает лестницу с четырьмя ступеньками, и отверстие квадратной формы, а конечный результат вы можете увидеть на Рисунке 57, где представлено множество линейных сегментов, созданных в виде скученных повернутых вправо треугольников. Чтобы покрыть эти сегменты квадратами. Мы должны утроить количество квадратов в каждом шаге. Из этого следует, что если d – измерение, то 2 в степени d = 3, так что d = 1.586.

Рисунок 57. Фрактальный треугольник, сформированный квадратами, поделенными на четыре части и собранных в правом верхнем квадрате, затем каждый квадрат был разделен еще на четыре малых квадрата и собраны в правом верхнем углу. Этот процесс повторялся много раз.
Если математики имели дело с фрактальными измерениями уже почти век назад, то для Бенуа Мандельброта оставалось только в середине двадцатого века, понять, что множества, имеющие фрактальные измерениям не являются странными, и что в действительности многие подобные системы существуют в природе ежедневно. Или по меньшей мере математические модели этих систем, имеюзих фрактальные измерения. Такие системы включают деревья со стволами и ветвями, листьями и соцветьями, а также горы со все более мелкими их частями. Существовала даже в свое время стать «Насколько длинно побережье Британии?» Что мы здесь могли бы заметить, так это то, что если что-то измеряется на очень больших детальных картах, то ответ становится все больше и больше. Этот эквивалент покрывает побережье все меньшими и меньшими квадратами и можно сказать, что ее значение где-то между 1.0 и 2.0. Мандельброт предположил 1,25.
Мандельброт ввел термин фрактал для описания системы с фракциональными измерениями. Береговая линия Британии и триангулярная структура на Рисунке 57 – это фракталы. Несмотря на судьбу других искусственных слов, данный термин быстро вошел в обиход и стал выражать сущность явления в одном значении.
Свойство многих фракталов в том, что Мандельброт постоянно обсуждал в своих статьях, это самопохожесть. Во многих фрактальных системах, с несколькими удобно расположенными кусочками, когда они увеличиваются, то становятся идентичными целой системе. Это значит, конечно, что несколько малых кусочков каждого кусочка при увеличении подобным этому целому кусочку и, следовательно, всей системе. На Рисунке 57 каждый маленький треугольник явно идентичен большой структуре. Другие фракталы только статических имеют самопохожесть. Малые кусочки, когда они увеличены, не представляют собой суперпозиции целой системы, но они будут иметь сходный тип при своем появлении. Такой фрактал появляется на Рисунке 58, созданный на манер Рисунка 58 за исключением того, что вместо правого верхнего угла каждый квадратик сдвинут с места.
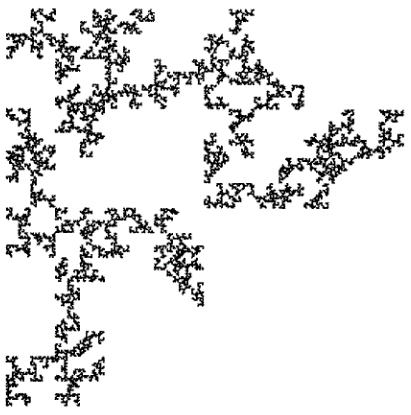
Рисунок 58. Фрактал, сформированный на основе Рисунка 57, но здесь каждый квадратик двигается сам по себе случайным образом.
Используя концепцию самопохожести вы можете сконструировать собственное фрактальное дерево. Если вы сместите множество или удовлетворитесь грубым наброском, то при этом даже не потребуется компьютера. Начните с вертикальной линии – это ствол. Затем сверху ствола нарисуйте линейные сегменты горизонтально в разные стороны, каждый вшестеро длиннее, чем сам ствол с ветвями. От каждого конца ветви нарисуйте прямой вертикальный сегмент сверху вниз, снова вшестеро длиннее самих веток. Продолжайте так по вертикальным и горизонтальным сегментам, пока линии не будут так близки друг к другу, что нарисовать их не позволит толщина карандашного грифеля. Умы можете получить нечто подобное Рисунку 59. Если бы вы смогли продлить процесс построения на бесконечное число шагов, то у вас бы получился фрактал с измерением 1.356. Листья, представляющие собой лишь точки на ветвях, также формируют фрактал с мерностью в 1.356.
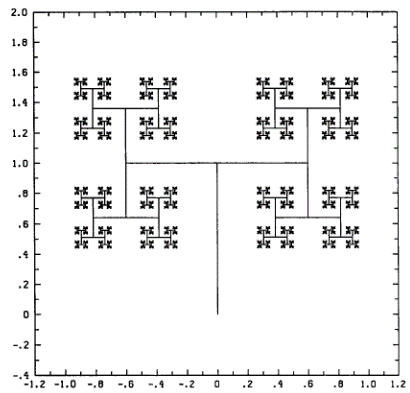
Рисунок 59. Фрактальное дерево, созданное вертикальными и горизонтальными сегментами по определенному шаблону и каждый сегмент вшестеро больше родительского.
Отношение длины ростка к стволу дерева не должно быть шесть десятых. Если вы уменьшите это меньше чем в половину, то листья сформируют фрактал с мерностью меньше, чем 1.0, даже несмотря на то что дерево будет выглядеть подобно тому, как на Рисунке 59. Если вы увеличите отношение до 0ю707, то есть корень из 1/2 , мерность достигнет 2.0 и дерево, как и листья будет заполнять треугольник. Нет пособа нарисовать плоскость с мерностью больше 2.0, а если вы сделает отношение больше 0.707, то более короткие ветви просто упадут сверху на более длинные части фрактала.
А что если сделать отношение точно в половину? Мерность будет точно 1.0, но дерево все еще будет выглядеть подобно тому, что изображено на Рисунке 59. Кажется разумным включить множество подобное этому в семейство фракталов, даже хотя их мерности «так уж получилось» - целые числа.
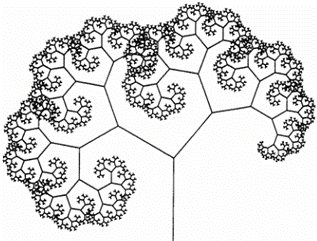
Рисунок 60. Фрактальное дерево, нарисованное по принципу Рисунка 59, за исключением того, что отношения вместо 0.6 скорее 0.7, а углы вместо прямых около 60 и 40.
Вы можете возразить, что рисунок выглядит скорее как перегруженный телефонный столб, а не дерево. Есть и другие мнение. В каждой ветви две меньшие ветви могут оставить родительскую ветвь под разными углами, не обязательно под прямыми, и их длины могут иметь различные отношения к длине родительской ветви. Также возможно, чтобы три или более отростка покинули ствол на разной высоте. Чем больше таких вариантов вы рассмотрите, тем лучше поймете, что на самом деле все это выглядит именно как дерево.
Рисунки 60 и 61 показывают две такие попытки. Они созданы в той же компьютерной программе, что создала Рисунок 59. Разница здесь только в выборе двух углов и двух отношений. Вы можете увидеть результат по наклонным отросткам и ветвям. Интересные структуры, не всегда естественные, можно создать также построив одни листья, как на Рисунках 62 и 63. Картинки кажется не слишком разделяют заявление Мандельброта, что фракталы, насколько их можно рассмотреть при определенном разрешении, богаты по своей природе.

Рисунок 61. Еще одно фрактальное дерево с отношение 0.75 ми 0.55 и углами 30 и 10.

Рисунок 62. Фрактальные листья дерева, где отношения 0.7 и 0.65, а углы 80 и 20.
Что общего у фракталов и хаоса? Совсем немного, а именно когда фрактал – это треугольник, созданный смещением правых верхних углов квадратов. В Рисунке 57, к примеру, ничего нет такого, что указывало бы на случайность. Самое большее, что можно сказать, это просто рутинная операция, создавшая фигуру, которая выглядит просто странно для любого, кто привык видеть фигуры лишь в учебниках по геометри.
Треугольники можно было бы даже назвать хаосом наоборот, если рассматривать альтернативную процедуру создания его. Это определение я впервые услышал на лекции, представленной Майклом Барнслеем из института Джорджии. Расположите три угла и постройте точку на любой из сторон. Выберите один угол случайно и постройте точку между первой точкой и этим углом. И снова выберите угол случайным образом и постройте точку между новой точкой и этим углом. После многих повторений этой процедуры вы получите треугольник на Рисунке 57. Самое интересно, что если вы выбираете углы в регулярной последовательности, вместо случайно, то закончите весь процесс за несколько точек. Таким образом, в реальном смысле, треугольник это нечто такое, что выглядит случайным, но на деле таковым не является.
Пока я говорю о треугольнике, давайте вспомни еще один способ его построить. Возьмем большой кусок бумаги, помеченный на маленькие квадраты. Поместим «х» или какую-то другую отметку в одном квадрате на верхний ряд. На следующем ряду и затем последующих рядах поместим отметку в квадрат если квадрат выше точки или левее отметки, но не когда сходятся оба эти условия. Как только будет сделано множество рядов, можно посмотреть на бумагу издалека и вы увидите среди отметок треугольник.
Процесс при котором каждый новый ряд включает предыдущий и использует его – называется маппингом, но не таким, как мы привыкли его видеть раньше. Он имеет бесконечное число переменных, представленных квадратами, которые формируют ряды, но существует только конечное число значений, которые можно допустить – только два в данном случае, связанных с «х» и пустым квадратом. Прогрессия от ряда ка ряду представляет собой развитие во времени. Такие систему называются клеточными автоматами, и они впервые появились как побочный продукт плодовитого воображения Джона Фон Нюмана. Интерес к ним частично был продиктован тем, что эти мерности появились при особых экономичных обстоятельствах, симулируя движущиеся потоки.
Некоторые фракталы очень близки к определению хаоса, поскольку созданы по некомплексным правилам, и не всегда знакомы по своей структуре. Однако существует очень близкое сходство между фракталами и хаосом в виде фракталов – странных аттракторов.
Для аттракторов, как на рисунках 12 16 с их комплексностью и почти параллельными кривыми, число малых квадратов, требующихся чтобы покрыть точку, будет более чем вдвое больше на сторону квадрата, порезанного пополам, поскольку каждый квадрат будет длиться, пересекая несколько кривых. Это не учетверение, поскольку все большие и большие дробления квадратов будут все больше пропадать между кривыми. Следовательно эта мерность лежит между 1.0 и 2.0.
Рисунок 64, созданный так ,что каждая вертикальная линия, проходит через пересекающее ее множество Кантора, чья мерность между 0.0 и 1.0, указывает на основание рисунка. Следовательно это можно использовать как шкалу для определение дробной части мерности таких структур, как рисунки 12 и 16, чьи пересечения с прямыми линиями представляют собой множества Кантора. Кто-то может заметить, что эти множества скорее разуплотнены слева и сплочены справа. Для мерностей от 0.1 и даже выше, допустимы только два пересечения с вертикальной линии при рисовании, что выглядит так, словно она состоит из двух объединенных поверхностей. Линии обрезаются на Рисунке 12 и 16 и выглядят как центральная часть шкалы, а аттрактор может быть определен по мерности около 1.5. Однако сравните это с обсуждение экспонент Ляпунова и мерностью в Приложении 2.

Рисунок 63. Другой пример листьев, когда оба отношения 0.71, а углы -70 и +70.
Немного схожая фигура, составленная из длинных кривых вместо случайно выбранной точек на этих кривых, появляется в интересной книге Мандельброта «Фрактальная геометрия природы». Здесь в действительности эти кривые, пересекающиеся с вертикальными линиями, представляют собой множества Кантора. Использование точек на Рисунке 64 предполагает усиление сравнение с другими рисунками, созданными точками, вроде рисунков 12 и 16.
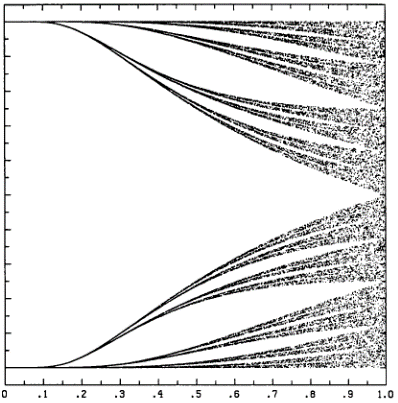
Рисунок 64. Фрактально-мерная шкала. Любая нарисованная вертикальная линия через фигуру будет пересекать ее в множестве Кантора, между 0.0 и 1.0.
Это было в конце семидесятых, когда слово «Хаос» стремительно завоевало свои позиции в качестве стандартного термина для феномена, описывающего ощутимую зависимость. Это было также то самое время, когда стали во множестве появляться различные странные аттракторы, и эти аттракторы с их фрактальной структурой, скорее периодичные, чем с ощутимой зависимостью, были вестниками некоторых важных научных открытий. По крайней мере временно они стали основной темой теории хаоса. Это был всего лишь краткий шажок в «хаос», не дающий представления об огромном семействе фракталов всех видов, и даже их основных форм. Особенно эта тема дала о себе знать, когда появились компьютеры. В ретроспективе буде трудно установить, что в самом начале значил «хаос», но представляется, что он охватывает многие области науки в тех или иных формах.
Остается один маленький вопрос о том, что хаос, как и страный аттрактор – это нечто, что устанавливается самостоятельно. Я часто размышляю над тем, как прекрасно назван бестселлер Джеймса Глейка – «Ощутимая зависимость: Создание новой науки».